任何非阻塞立方体的集合,其总体积不超过1/3,都可以装入单位立方体。
设一个d维立方体,为,设一个边长为1的d维立方体。我们说,如果有可能对集合应用平移和旋转,那么这些立方体就可以被装入,这样得到的平移和旋转的立方体就包含在相互不相交的内部。如果任何填充立方体的每条边平行于的边,则该填充是平行的。
Meir和Moser(1968)证明了任何d维立方体的集合都可以平行装入单位d维立方体中,只要立方体的总体积不大于。这个上界对于平行填充是尖锐的:不可能将两个边长度大于1/2的d维立方体填充到一起。特别是,边长大于1/2的两个三维立方体,因此,总体积大于,不能平行装入。一般情况下,任意两个边长之和大于1的立方体在平行填充中相互遮挡;如果我们装一个,就没有足够的空间装另一个了。在本文中,我们将从满足附加条件的集合中打包三维立方体。
我们说立方体是非阻塞的,如果对于任何(比较Januszewski和Zielonka 2023a)。在Januszewski和Zielonka (2023b)中表明,任何总面积不超过5/9的非方块集合都可以被填充。本笔记的目的是证明任何非阻塞立方体的集合都可以被平行装入,只要这些立方体的体积总和不大于1/3。这个上界对于平行填充是尖锐的:9个边长大于1/3的立方体不能被平行填充。
第3节中介绍的包装方法是基于Meir和Moser(1968)的著名方法。一开始,立方体是按大小排列的,从最大的开始。然后立方体被打包成连续的层,这样它的底部就被打包成正方形。因此,我们将首先描述填充方形的算法。
这里的和是指矩形。我们将使用Januszewski和Zielonka (2023b)中描述的方法,这是Moon和Moser(1967)算法的稍微修改。为了方便读者,我们将提供一个如何包装正方形的草图。
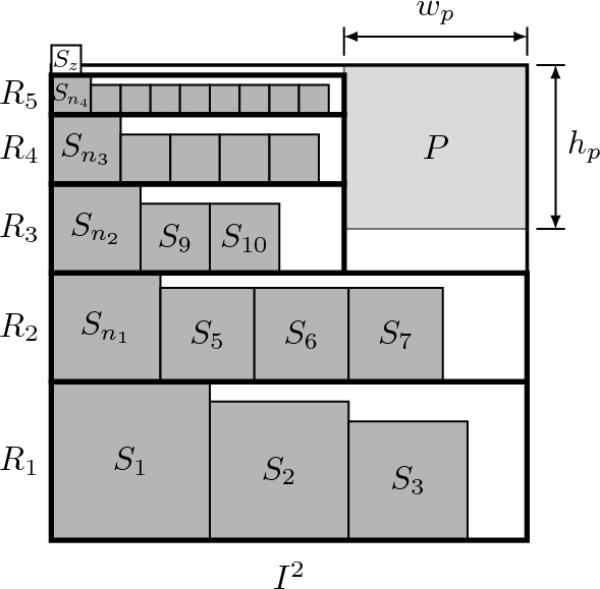
包装方法
设和为正方形的集合,其中为和的边长。此外,假设(见图1),其中和。通过表示P的内部。
正方形是分层排列的。第一层要么是矩形if,要么是矩形else。这些方块从左到右排列在第一层的底部。如果是第一个不能以这种方式填充的正方形,那么新的高度层就直接在上面创建。的底要么等于1,要么等于。这些方块从左到右排列在第二层的底部。如果第一个正方形不能以这种方式填充在第二层中,那么新的高度层将直接创建在第二层的上方。的底等于1,否则等于,等等。
如果是第一个不能用-方法填充的正方形,那么正方形的总面积加上P的面积大于
假设方块被填充而不能用-方法填充。为了证明这个引理,只要证明面积的平方可以被和P覆盖并有一定的余量(即和P的面积之和严格大于)就足够了。设(见图2)。
让我们将图层中的第一个正方形移动到正后方的位置,使的左下顶点是的右下顶点(如图2中左侧的白色正方形)。然后我们将正方形从(没有但有)向上移动距离。此外,我们从层(连同)向上移动正方形的距离,为(见图2,右)。
需要注意的是,有了这种正方形的排列,每个正方形的右侧都在层外为。此外,。这意味着和P允许覆盖有一些多余的(见图3)。

填充方形的总面积的估计

引理1,当
这里的,where, and,是指盒子。填充法是对Meir和Moser(1968)算法的一个小修改。
让。另外,设为一个边长为的立方体,其中为,设。假设(见图4),其中,和。
立方体被打包成H层,类似于Meir和Moser(1968)的方法。每一层的底部是一个单位正方形。第一层是盒子。根据-方法,将立方体装入,以便立方体的底部装入层的底部。如果,则在-方法中,否则。如果第一个立方体无法装入,则在其上方直接创建一个高度为1的新层。根据-方法,将下一个立方体装入,以便立方体的底部装入层的底部。如果,则在-方法中,否则。如果第一个立方体不能在第二层中以这种方式填充,那么新的高度层将直接创建在第二层之上,依此类推。
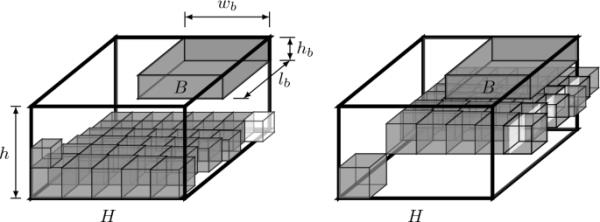
估计包装立方体的总体积
如果是集合中第一个不能用-方法装入的立方体,则立方体的总体积加上B的体积大于
假设立方体是通过-方法打包的。注意,为了证明这个引理,只要证明箱子可以被和B覆盖并有一些多余的部分就足够了。让。
让我们移动(图层中的第一个立方体),这样底部的左下顶点就是底部的右下顶点(如图4中的白色立方体左侧)。然后我们将立方体从(没有但有)向上移动距离。此外,我们将立方体从(with)向上移动距离,为(见图4,右)。现在我们在每一层中移动立方体,使这些立方体的底部以与引理1证明中描述的相同的方式放置,即立方体底部和矩形P(如果有的话)的并集覆盖层底部的正方形。
需要注意的是,在这种立方体的排列方式下,每个立方体的右面要么在b的外部,要么包含在b中。这意味着和B允许在箱子上盖上一些多余的东西。
设和为立方体的集合,设和,其中为的边长
让
显然,如果,那么B是一个大小相同的盒子。
前四个立方体,即,和被装入U的上角,以便包含B(见图5,左)。
如果,则没有更多的立方体将被装入U中。否则,我们将尽可能靠近顶部装入U中。除了和没有更多的立方体将被装入U。
通过-方法(如图4所示)将剩余的立方体打包到相应的层()中。

非阻塞立方体的包装
任何体积不大于1/3的非阻塞立方体的集合都可以装入单位立方体。
用集合中的多维数据集表示。在不失一般性的前提下,我们可以假设,其中为的边长
我们将证明,如果立方体不能装进去,那么,这是一个矛盾。很明显,(if, then和block)。考虑两种情况。
情况1:。
B的体积等于。如果立方体不能被装入,那么,根据引理2,立方体的体积总和大于
求函数的全局最小值
在以下不等式给出的定义域内
因为和,平稳点在定义域之外。
三角形的边界由三段组成。
的片段。这个函数
为增加。这意味着。
的片段。这个函数
为增加。因此,。
的片段。这个函数
为达到其最低值。
因此,函数f在给定定义域内的最小值等于1/3。
案例2:。这意味着它被打包进了美国。
如果立方体不能被装入,那么,根据引理2,立方体的体积总和大于
求函数的全局最小值
在以下不等式给出的定义域内
所有四个静止点
都在域外。
的边界由三段组成。
的片段。这个函数
为达到其最低值。
的片段。这个函数
为达到其最低值。
的片段。观察到
对。
因此,函数g在给定定义域内的最小值大于1/3。
在包装立方体分组成批(比较Januszewski和Zielonka 2022和Januszewski和Zielonka 2023)。数据集在线到达并存储在缓冲区中,直到存储的数据集的总体积大于或等于或所有数据集都已到达。然后将缓冲区中的多维数据集脱机打包到单位容量桶中,并清空缓冲区。下面的问题出现了:什么是最小的,使得任何体积不大于1/3的非阻塞立方体的集合都可以装进去?
发表评论
暂时没有评论,来抢沙发吧~