顶吹过程中金属液滴向炉渣中喷射是转炉过程的特征。熔渣中金属液滴的停留时间对熔渣反应动力学有重要影响。本文研究了转炉炼钢过程中喷出金属在炉渣中的停留时间,并对基于吹数理论和质量平衡的各种方法进行了比较。以前发表的吹数理论与基于物理的上限和下限进行了比较评估。结果表明,只有部分实验室规模的吹风次数相关性适用于工业吹风条件。建立了一个数学模型来预测质量分数的返回率,从而预测液滴在渣乳中的停留时间。结合先前发表的喷射液滴尺寸分布模型,可以预测金属-渣反应界面面积和传质条件的动态变化。
碱性氧炼钢的精炼反应主要发生在气喷冲击区、乳化液-金属界面和渣-金属乳化液中。在乳化液中进行的精炼过程的意义是根据观察到的,即乳化液中金属液滴中的碳和磷含量远远低于体中的碳和磷含量来解释的。[1]利用冷模型和热模型估算了参与精炼的液滴的质量喷射率。[2,3]然后提出了将气体射流动量和喷枪距离与喷射金属质量联系起来的公式。[4,5,6,7]由于氧射流与泡沫和膨胀射流与液态金属表面的复杂相互作用,对质量喷射速率的准确预测是困难的。为了确定乳化液精炼动力学,必须考虑三个参数:喷射到炉渣中的总质量、喷射液滴的大小分布和液滴停留时间。结合这些量,假设金属液滴在炉渣中停留的时间不影响其尺寸分布和形状,则可以推导出乳状液的性能。虽然已有研究表明Fe-C液滴在精炼反应过程中会破裂[8,9],并证明了在近乎停滞的炉渣中液滴会膨胀或膨胀[10],但在考虑一步乳化脱碳反应路径时,对于非常小的液滴甚至较大的液滴,都可以使用致密液滴理论。所提出的模型可用于估计反应速率,或作为涉及进一步现象的更全面的过程模型的基础。
本研究旨在开发一种计算效率高的建模方法,可用于估算转炉过程模型中的金属-渣界面面积。用工业转炉的实验数据对模型进行了验证。
考虑到当今的经济和生态挑战,研究人员越来越有必要关注并获得对现有精炼工艺的新见解。为了优化对炼钢现象的理解,研究人员需要创新的方法和对正在发展的新精炼工艺的新见解。
图1显示了物质喷射过程和乳化液精炼的思想模型。每隔一段时间喷射出一定的热金属。已经提出了各种相关性来预测喷射速率,[5,6,7,11],但Subagyo等人[7]提出的blownumber理论和Rout等人[11]提出的修正理论可以说是最近文献中最流行的。喷出的物质以不同大小的金属液滴的形式转移到炉渣中。喷射质量的表面体积比与精炼动力学有关,当液滴在其停留时间内未与炉渣达到平衡时。最近,研究表明,抛射液滴的重量分布,也称为抛射液滴种群的质量密度函数,可以使用质量-弹簧振荡器模型很好地预测。[12]在特定时间乳化进入吹风的铁水质量取决于吹风条件和炉渣性质。在乳液流入和流出的稳态条件下,半径为和的液滴之间的液滴分数的停留时间可通过式[1]求得。
(1)为静态条件下被炉渣支撑的液滴数量的质量密度函数。和是考虑的质量密度函数的分数的极限。分离驱动力与单个液滴的质量成正比。质量较大的液滴在炉渣中的停留时间比质量较小的液滴要短。这种现象可以用特定的液滴返回率来描述,这是每单位时间内从乳液中丢失的液滴到大块热金属中的比例。为了适用这一点,假定液滴具有恒定的密度,并且在任何时候都均匀地分布在炉渣中。因此,如果在乳液的任意位置取足够大小的样品,则样品中的金属液滴尺寸分布保持不变。液滴回吐率是准确描述金属渣乳状液的关键因素。本文提出了一种经过验证的建模方法。
金属液滴在空腔区喷射的示意图
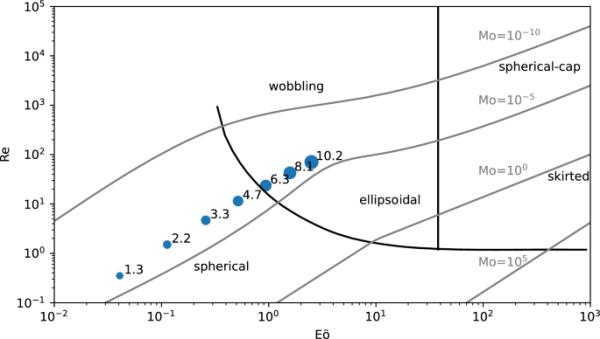
人们观察到,在氧化渣中的液态铁液滴周围形成了一个气晕。[13]通常计算乳液脱碳时,假设反应路径为两步,如图2(a)所示。最初,氧气通过炉渣-气体界面传递,将一氧化碳氧化为二氧化碳。然后,二氧化碳被转移到气-金属界面,为随后氧化溶解在铁液滴中的碳提供氧气。这一机制预计将适用于停滞渣中的小液滴,这些液滴具有较低的终端速度,因此行为类似于刚性球体。然而,如果炉渣高度搅拌或液滴大到足以落下形成后尾迹,则铁碳液滴可能通过一步反应路径脱碳(如图2(b)所示)。在液铁液滴在炉渣-金属界面上的驻点处,氧从炉渣转移到金属液滴,导致一氧化碳局部过饱和溶液。这个过饱和层遵循假定的内部流线[14],流向气-铁界面上的第二个停滞点。当液滴内的液体过饱和层到达三流体线(气-渣-铁)时,就发生脱碳反应。
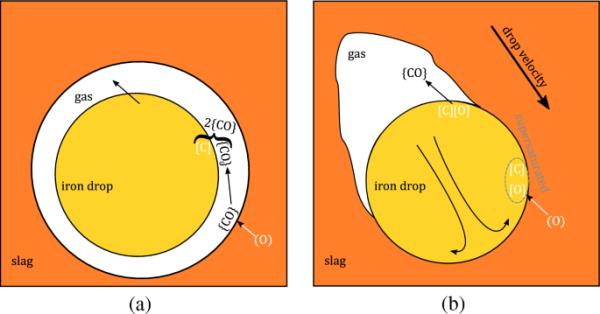
乳液脱碳途径为(a)间接[15]和(b)直接反应途径
金属渣乳状液脱碳过程的确切反应机理至今仍有推测。新引入的反应模型为搅拌乳化条件提供了进一步的可能性,但缺乏实验证据。
利用各种经验方程计算了金属热物质喷射到乳化液中的速率。这些方程通常是从使用约1:1000的体积比例的水模型推导到今天的工业转换器。为了验证模型的有效性,研究了弹射速率上限和下限的估计方法。
质量抛射率的下限可以通过磷的质量平衡来估计,假设脱磷只发生在乳状液中。Resch[6]提到通过渣的铁水质量通量的周转量可以通过在吹炼和吹炼的两个特定点取样块状和乳化液来计算。假设在两次取样期间,渣渣的总体质量没有显著变化,可以使用磷平衡来估计渣渣中液滴的质量流。稳态条件下,质量抛射率近似为:
(2)式中为金属浴的质量,和为上述点和处金属浴中磷的重量分数,和为水滴从体中喷射和返回体中的磷的重量分数的时间平均值。
式[2]中分子的预期误差较低,这是因为假定体磷由于热金属体的充分混合而均匀分布。体积的质量可以假定为恒定的,也可以通过质量平衡加以修正。当在短时间内取样时,热金属质量变化的速率可以忽略不计。喷射出磷含量的平均值可估计为体积磷在和之间的平均值。因此,与喷出的物质的时间平均磷浓度相比,可以准确地估计出体积的磷含量。这些量中最大的不确定性是当液滴返回体积时的磷含量。可以假设在乳状液取样过程中(20秒[6]),脱磷反应仍在继续。这导致相当一部分液滴精炼归因于取样程序而不是过程本身。根据Resch[6]的计算,发现停留时间接近2秒。因此,废渣-金属乳化液中提取的金属液滴所分析的磷含量可以且应该被忽略。如Resch所述[6],液滴中的磷含量已经接近平衡状态。假设在乳状液精炼过程中发现了转炉脱磷,则只能对较低的喷射极限进行估计,而不能进行质量喷射预测。
(3)式[3]给出了最小质量抛射率的估计,假设落回体中的液滴含磷量为零,且平均抛射磷量与体中平均抛射磷量相等。这导致在分母中磷的差异的一个较高的估计。由于已知分子中的物理量具有较高的精度,因此所得到的量是所期望的物理变量的下限。
金属热物质抛射的原因是气体射流对金属热表面的撞击。喷枪上的喷嘴设计用于提供具有高动能的射流,从而在吹打过程中允许连续的气体-金属接触。射流的功率可以用等熵流动方程来近似计算。利用自由湍流射流理论计算了射流在喷枪高度处的定向动能功率。流体流动随速度和质量通量的幂如式[4]所示。
(4)为了估计液滴质量喷射速率的上限,我们假设,在距离喷管类似喷枪高度的距离处,从体积流出的热金属质量流的功率必须小于自由湍流条件下类似气体射流的功率。根据下式计算出出体质量流的功率
(5)式中表示以半径为半径的球形液滴离开热金属体的初始速度。对于小液滴,这个速度主要受边界层动量的影响。在较大的液滴中,被控制的影响作为起飞前类似质量的振荡速度。利用Mitas等人提出的质量-弹簧替代模型估计液滴的振荡速度[12],然后利用这两种速度的动量加权速度计算具有半径的球形液滴的出口速度。Koria和Lange[2]实验装置计算的液滴出口速度与Subagyo[16]使用该模型计算的液滴出口速度对比如图3所示。对于非常小的液滴,出液动量受液体边界层动量的支配。对于较大的液滴,通过函数的强曲率进入一个过渡时期,如图3所示。当液滴直径更大时,液滴出腔时的动量越来越不受边界层动量的影响。
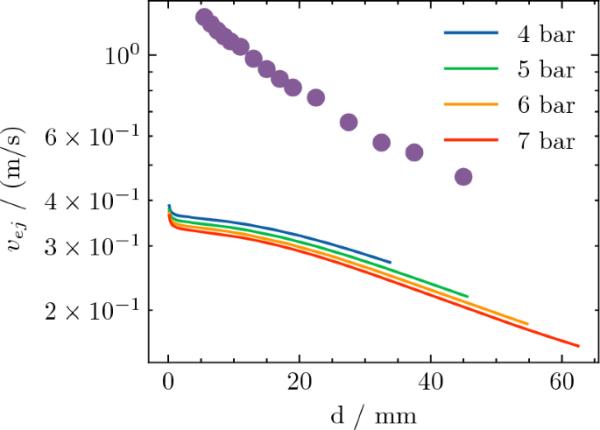
在无量纲喷枪高度为37.5的情况下,不同供给压力(4,5,6和7bar)下金属液滴的出口速度与液滴尺寸的函数关系。Subagyo等人[16]使用Koria和Lange[2]的实验值(标记)计算的值与Mitas等人[12]使用振荡器模型计算的值的比较(连续线条)
图3所示液滴出口速度的计算值与Subagyo等人报道的数值在同一个数量级。[16]对于非常小的液滴,出口速度接近热金属的动量边界层速度。对于直径在20-40 mm范围内的液滴,计算值的梯度与Subagyo等的计算值梯度相似[16]。
为了估计液体抛射的上限,将式[5]与式[4]结合,得到式[6]。喷射速率上限由式[6]计算,适用于200吨转炉,如图4所示。观察到,降低喷枪高度可增加作用于表面的气体射流的最大功率。液滴尺寸分布向较大的液滴转移,液滴的出口速度增加,导致每喷射质量的动能要求更高。这个比能量是导致与较低枪高相关的较低最大弹射值的主要影响因素。
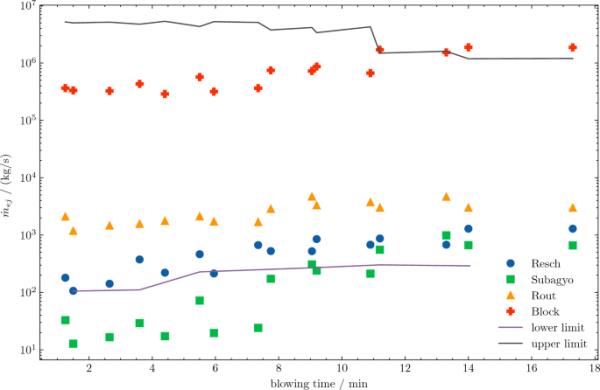
根据各种吹数理论计算质量抛射率,根据方程计算质量周转上限和下限。[3]和[6],应用于200吨转炉的数据。[6]
(6)所观察到的喷射速率如此之高,以至于喷枪高度无法维持,尽管停留时间很短,如图4所示。尽管如此,在展示概述时,枪的高度并没有被修正。这使得评估某些质量抛射模型的适用性成为可能,没有对喷枪高度进行修正。Block等人[5]和Subgyo等人[7]的模型得出的结果与所提出的限制相冲突,这意味着它们不适合预测所研究的200吨转炉的喷射速率,基于所研究的案例,Block[5]和Subagyo等人[7]的模型很可能只是定性地描述了工业转炉中金属液滴的喷射行为。Rout等人[11]的模型本质上是Subagyo等人[7]的吹数相关性的修正。在高温环境下,产生的喷射率落在下限和上限之间,因此在数量上是合理的。
在稳态条件下,由等大小液滴组成的金属液滴群的停留时间可计算为:
(7)式中为悬浮在炉渣中的金属质量,表示金属质量喷射到炉渣中的速率。如文献17所述,式[7]中的表达式符合利特尔定律[18],该定律对任何稳定的抢占系统都有效。
给出金属-渣乳化液样品,并对样品中金属与渣的质量分数进行评估,就可以估计出乳状液中金属的总质量。对渣质量的预测比对金属分数的预测更准确。当通过中断吹炼和倾斜转炉来取样时,质量较大的液滴会分离,无法回收。最重的液滴在喷射分布中占最大的重量分数。考虑到采样过程,Resch[6]提到的采样检索时间为20秒,这是非常快的,但是对于检索具有代表性的大小分布来说仍然太慢。正如Resch[6]进一步提到的那样,这导致了对乳化热金属质量的低估,从而导致了质量加权停留时间的低估。由Resch[6]通过Eq.[7]计算出的停留时间如图5所示。
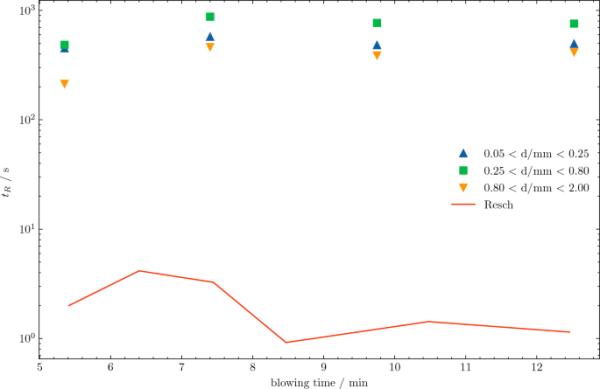
根据Resch使用式[7](线)计算的停留时间与使用式[8]计算的200吨工业转化器不同液滴大小分数(标记)的停留时间进行比较
如果喷射液滴和乳化液液滴种群的大小分布已知,则具有半径的液滴的停留时间可计算为:
(8)其中总渣重可以通过磷质量平衡来估计。弹射尺寸分布采用Mitas等人[12]提出的模型计算,静态尺寸分布采用Resch的实验数据[6]。为了获得可比较的结果,根据Resch计算了质量抛射率。[6]
在图5的尺寸范围内,液滴的重量分数远低于物理检索样品的分析值。只有少数大液滴会将重量分数移至较低的值,导致停留时间大大缩短,如图5所示。正是这些液滴在提取乳剂样品之前回到了大块的热金属中。这被认为是图5中显示停留时间的主要因素和原因。似乎很高。由Resch计算的物质抛射率是可能的,尽管实际值可能更高。静态条件下的乳化质量肯定比计算时所取的值要高。这种影响,而不是前两种影响,会导致更长的居住时间。
假设所有大小的液滴均匀分布在整个炉渣中,就可以描述热金属质量从乳状液流入体中的过程。利用这一假设,可以计算出基于乳液体积的液滴回流率。如果每隔一段时间将乳化液的一个体积单元的半径液滴排空,则从体积乳化液中流出的液滴质量如式[9]所示。
(9)这是提出的金属渣乳状液中液滴回流率的定义。这个物理量的倒数是停留时间。
(10)在转炉过程中,炉渣乳化液中不仅充满了吹扫气体,而且有一部分脱碳产物是在乳化液中产生的。为了描述这种乳化泡沫,将转炉区域建模为直径等于转炉容器半径的气泡柱组成的电池。采用Zehner[19,20]的解析模型对气泡柱进行表征。图6显示了转换器中直径为1的气泡柱。这里显示了柱轴中心的向上流动和气泡柱外缘的向下流动。根据该模型得到的涡流速度如式[11]所示。

停留时间模型的示意图
(11)气泡柱的几何形状限制了最大涡流的大小。给定涡流速度和涡流尺寸,计算角速度以及四分之一旋转所需的时间。对于每个液滴尺寸,假设沿二维涡流径向分量的分布是均匀的。在涡流旋转四分之一之后,一定比例的液滴已经离开了乳液。该分数由式[12]表示,用于描述在上述四分之一旋转过程中失去液滴的乳液的体积分数。
(12)使用前面的等式。[9]、[10]、[12],则停留时间可根据式[13]计算。
(13)其中,表示从涡流旋转原点到乳化液液滴空洞区域开始的距离。在这个位置的液滴将相对于炉渣移动,在四分之一旋转期间的距离,因此是极限实例。最初远离中心的液滴将被热金属体消耗,而靠近旋转中心的液滴将不会到达炉渣-金属界面。
液滴的运动可以通过求解二阶非线性运动方程来计算,考虑重力和离心力为驱动力,阻力和黏性力作用于液滴。对于在200t转炉吹气过程中喷射出的液滴群(例如,由Resch[6]分析),粘度和阻力都不能安全地忽略。
忽略液滴的加速阶段,计算沉降速度[21]S.106(6.1)如式[14]所示,计算强度较小。
(14)该方程稍作修改,加入了如式[15]所示的离心加速度。
(15)通过在数值最小化程序中执行式[13],可以计算出每个液滴直径的停留时间。
上一节介绍了给定半径r的液滴停留时间的建模,考虑到液滴种群的停留时间,多个数量可能是重要的。图7描绘了一个假想的喷射液滴分布。它由两种大小的液滴组成。每秒钟一个大液滴和一个小液滴喷射到炉渣中。大液滴平均在2秒后返回到块体,而小液滴的停留时间要长4倍,导致它们在渣金属乳状液中堆积。显示的箭头不表示轨迹,只表示退出和返回批量。

假设喷射群由两种大小的液滴组成:较小的液滴停留时间为8秒,而大三倍的液滴停留时间为2秒
液滴种群的质量加权停留时间可由式[16]计算。当反应动力学受到大量供应的限制时,这种停留时间将证明是相关的。
(16)界面面积加权停留时间的计算方法类似于式[16]。利用液滴的单个表面积。当反应速度明显依赖于交换面积时,这个物理量是有用的。
(17)计算采用稠密液滴假设,特征液滴封存涡流由容器的几何形状和数量定义,如表1所示。空管速度采用乳化液脱碳效率来计算每个转化器圆柱面产生的一氧化碳体积。利用实测的炉渣化学成分[6]和urban黏度模型的Mudersbach修正[22]来计算炉渣黏度。假设炉渣温度比铁水温度高100℃。考虑了化学成分和温度对炉渣粘度的影响,忽略了固体分数和炉渣密度的影响。
等式中描述的原则。将[16]和[17]应用于Resch[6]分析的200吨转炉,结果如图8所示。200吨转炉采用氧枪共喷石灰。作者[6]没有提到底吹技术的使用,这是已知的提高质量抛射率[3]。因此,在后面的计算中没有考虑底吹对抛射率的影响。

将喷射液滴种群的停留时间与Sarkar[23]的计算结果和Price[24]对不同液滴分布上限因子值(a) 1、(b) 1/4、(c) 1/16和(d) 1/64进行的测量结果进行比较
采用乳化液脱碳的方法,将炉渣中气体流动与供氧有效地联系在一起,作为一个常量进行整体计算。因此,在吹塑结束时减少脱碳对停留时间的影响没有在图8中看到。尽管如此,由于炉渣粘度的变化,停留时间仍有衰减。从图8中可以看出,质量加权停留时间与液滴分布上限有很大关系,因此也与Constant有关。当这个模型常数从1变化到1/64时,质量加权停留时间不成比例地变化。正如预期的那样,界面面积加权停留时间变化相对较小。这是由于较小的液滴(占整个表面积的大部分)保持不变。从转炉过程质量平衡计算的角度来看,小液滴的停留时间可能超过转炉的总精炼时间,因此它们在炉渣中丢失。图9描述了攻击后9.2分钟的停留时间。可以观察到,在尺寸下限附近的液滴的停留时间超过10,000秒。为了可视化细化与界面面积成正比时相关的液滴种群停留时间,在只考虑停留时间小于1000秒的液滴的情况下,计算了喷射液滴种群的界面面积加权停留时间。换句话说,只有在其他不变条件下能够返回到热金属体的液滴在进一步的打击中被考虑在内。熔渣中液滴损失的数量主要取决于停留时间较短的吹炼结束阶段。这也可能意味着,由于炉渣性质的变化,几乎永久地被困在炉渣中的液滴可以返回到金属中。
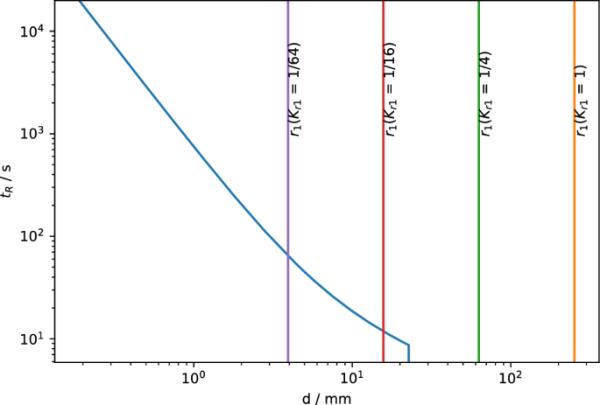
喷射出的金属液滴停留时间为9.2分钟。液滴分布上限为、和
图9描述了停留时间与液滴直径的关系。亚毫米级液滴停留时间大于1000秒。大液滴的停留时间较短,因为该模型在通过金属-渣边界时液滴的渣空穴率较高。喷射液滴种群的上端以不同的值表示。可以观察到,在和之间到达一个点时,模型不再产生停留时间。这一点标志着液滴的直径,当液滴从所考虑的乳化液涡流的原点开始时,在涡流旋转四分之一的时间内到达渣金属界面。
图10。描述了直径为2mm (a)和0.5 mm (b)的单个液滴的停留时间。建模的停留时间与Dogan等人的计算结果[25]以及公式[8]中给出的基于质量平衡的方法进行了比较。对于给定的半径,较大的值导致较小的质量分数。由于Eq.[8]中的质量密度函数在分母中,因此值越大,停留时间越长。在本模型和质量平衡模型下,半毫米直径液滴的停留时间比2毫米直径液滴的停留时间要高。当使用图10(a)和(b)比较等值的停留时间时,可以观察到,对于图10(b)中较小的液滴,每个值的停留时间都较大。估计的停留时间通过。方程8对液滴分布上限很敏感。另一方面,可以观察到Dogan等人[25]的模型和本模型都在通过低音平衡方法验证的实际停留时间范围内。然而,也有可能评估喷射液滴尺寸分布常数与模拟结果的关系。为了在这种情况下获得有效的结果,有必要假设当前模型的值在1到1/4之间,而Dogan等人的模型的值在1/4到1/64之间。[25]对于2毫米液滴,所有提出的公式都预测了在打击结束时停留时间的减少。对于半毫米液滴,当使用Dogan等人的模型时,停留时间在吹气结束时发生了显著变化。[25]当使用本模型和Eq.[8]中的质量平衡方法时,这种现象不那么明显。当使用质量平衡方法时,2毫米液滴的停留时间衰减大于半毫米液滴。
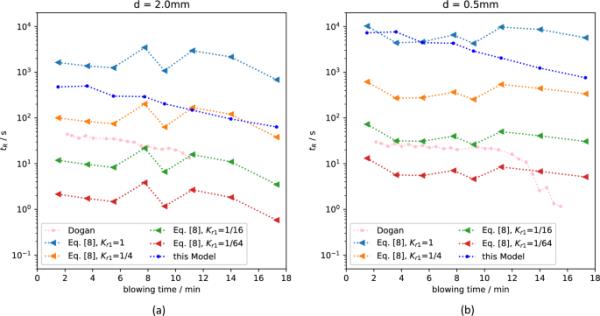
停留时间取决于单个液滴(a) 2 mm和(b) 0.5 mm的吹风时间方程[8]
图11显示了吹风9.2分钟时相对于炉渣的液滴移动量(Resch[6]“Schmelzengruppe 1”)。为了可视化,将液滴分布分为七个部分,图11中所示的每个点表示所显示液滴部分的相对权重。在刚性球行为区域之外发现了相当大的重量份额。因此,液滴内部循环和液滴外部形状在液滴通过炉渣运动过程中的变化对液滴与周围环境的传质起作用。小液滴对炉渣的相对速度较低。因此小液滴的变形力比大液滴小。表面张力趋向于使表面积最小化,在近乎停滞的炉渣条件下形成接近球形的液滴。从图11可以看出,在当前计算条件下,对于≥1/16的较高种群因子,计算得到的液滴种群的液滴没有到达球帽形成的区域。

气泡和液滴在液体中无阻碍重力运动的形状状态[26],金属液滴的叠加值假设为=1/16
由于喷射出的液滴尺寸随量级而变化,并且根据图11要考虑几种形状,因此当液滴尺寸分数的相对精炼重要性未知时,必须实施各种传质模型。
测量的精炼率可以用来验证模型。由于脱磷只发生在炉渣-金属界面,因此选择此精炼反应进行模型验证。金属体中磷的变化可由式[18]计算。因此,液滴中某种物质的浓度通常是液滴半径和反应时间的函数。更具体地说,反应时间也是液滴半径的函数。
(18)显然,精炼率取决于三个项的乘积。在Eq.[18]中给出的测试用例(9.2分钟后,“Schmelzengruppe 1”)的产品的对数如图12所示。

重要性因素:种群相对质量分数(),停留时间内浓度变化(),停留时间倒数:(a)整个液滴种群,(b)液滴大小6 - 11mm
很明显,最小液滴的精炼贡献可以忽略不计,因为它们的停留时间长,因此渣和金属块之间的质量交换率很差。停留时间逆的对数,即log10(1/tR),是小液滴直径时堆栈的最大元素。因此,它也是精炼性能的最大抑制剂。当考虑大液滴的分布分数时,它们较差的脱磷效果被较短的停留时间和较高的质量分数所补偿。从小滴到大滴,橙色的堆叠元素减小了它的大小,而绿色的堆叠元素增大了它的大小。从直径约5mm的液滴到直径更大的液滴,总的精炼抑制作用几乎是恒定的。图12(b))表明所显示的函数显示最小值。对所呈现现象的数学分析显示在附录中。液滴返回浓度取决于所采用的动力学模型。由于喷射出的液滴在大小和相对速度上与炉渣有很大的不同,因此采用了各种模型。
图13说明了在各种实现的传质模型中,抛射落总体的相对和累积脱磷。描述内部有限传质的模型有Handlos和Baron[14]、Calderbank和Korchinski[27]以及扩散控制传质。本文采用Frössling、[28]Higbie[29]和Wakao and Kagei[30]中的模型来探讨外部限制情况。阅读图13和图11可以得出结论,足够小的液滴实际上对精炼率没有贡献。因此,在良好的近似情况下,可以忽略纯扩散控制模型的实现。Calderbank和Korchinski[27]的模型描述了液滴体系中振荡液滴区域的传质过程(见图11)。由于考虑了内部流体循环,Calderbank和Korchinski[27]使用该模型预测的传质速率比扩散控制情况下的传质速率要快得多。使用Wakao和Kagei[30]、Handlos和Baron[14]以及Higbie[28]等模型预测的精炼率差异很小(见图13(d)),这表明与式[18]中的其他影响因素相比,所有模型中的传质足够相似,尽管对于所有计算状态,外部传质对估计的总体传质的影响< 5%。
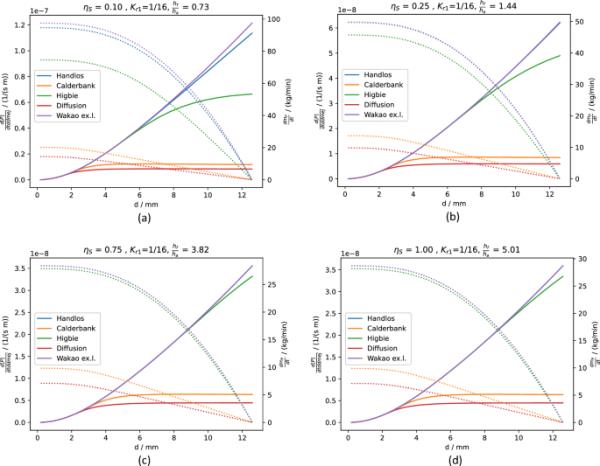
不同乳化液脱碳效率值(a) 0.1, (b) 0.25, (c) 0.75, (d) 1时,直径d的液滴对整个液滴群的精炼(实线)和由于乳化液精炼而导致的散装金属的累积除磷(虚线)的相对重要性
大块铁水的总脱碳有一定比例发生在乳状液中。这个分数称为乳液脱碳效率。利用发泡指数模型,可以在假设气体在随机位置产生的情况下计算出泡沫乳液的高度。因此,平均有一半的炉渣体积灌注了脱碳产物。图13显示,当脱碳完全发生在乳液中()时,泡沫高度需要是转炉中泡沫可用高度的五倍。即使在25%的乳剂脱碳时,也会发生漏液。
利用模拟的液滴半径停留时间和喷射金属的质量分数,计算了熔渣中金属液滴的总相互作用面积或界面面积。工业200t变流器的试验条件结果如图14所示。计算出的界面面积在量级上与其他研究人员相当。例如,Lytvynyuk等人[31]对200吨转炉进行了计算,假设界面面积为1000 m2,而Bundschuh[32]在主打击期间应用了1000至5000 m2之间的值。
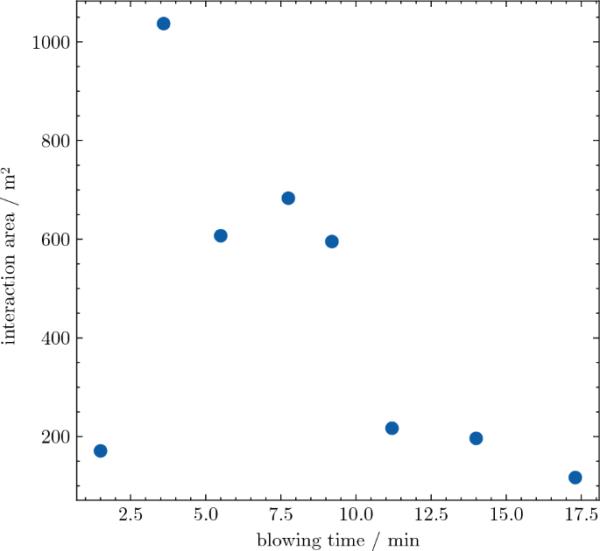
熔渣中金属液滴的总界面面积
转换器研究中面临的巨大物理挑战迫使专家们探索和依赖复杂的模拟。然而,有必要说明的是,使用降低复杂性的模拟可以产生有趣且足够准确的结果。
在转炉炼钢条件下,计算了液滴在炉渣中的停留时间。采用Zehner[19,20]的气泡柱模型来描述金属渣泡沫乳化液。液滴固存现象是通过力平衡来模拟的,从而导出了动力学方程。这使得计算各种液滴种群的停留时间以及任何给定大小的单个液滴的停留时间成为可能。停留时间与许多动态转炉模型的结果相当。结果表明,该停留时间模型具有较强的适应性,可以集成到在线动态转炉模型中。
在分析现有文献时,很明显,由于氧气射流的撞击,物质抛射的模型证明是模糊的。目前在已发表的文献中提出的物质抛射率的科学公式证明,当应用于工业规模的转换器时,差异很大。在本文中,通过将计算值与制定的物理极限相关联,对计算值进行了比较和验证。文献中可用的吹数相关性被发现部分地与这些边界相冲突。
在现有的文献中提到,乳状液中的液滴精炼是整体精炼中需要考虑的关键方面之一。通过缓慢采样方法(> 10秒)提取的液滴被认为是乳状液精炼的原因。使用基于这一思想开发的停留时间模型表明,使用缓慢采样方法充分接近的液滴正是在液滴精炼中不起作用的液滴。由此得出结论,只有直径大于2毫米的液滴才能对乳状液的精炼起作用。对于明显较大的液滴,液滴均匀分布的假设是不成立的。由于高质量交换率(较短的停留时间)和较大的液滴在总喷射金属质量中所占的高质量比例,大液滴在精炼过程中仍然发挥着至关重要的作用。另一方面,导致“乳状液精炼”术语的小而精细分散的液滴对总精炼的贡献可以忽略不计。在矿渣中存在一种分散的小铁滴乳液,但没有相应的固有精炼。
Resch[6]和sch
无论计算是用密集的还是膨胀的液滴进行的,小液滴的精炼性能都很差,因为它们与大块的质量交换率很低。这也适用于液滴“爆炸”成非常小的液滴的假设情况。在液滴遭受不可逆破碎后,它们的质量碎片没有足够的小停留时间来解释显著的精炼。与停留时间相比,胀气时间较短。大液滴的相对速度太高,无法形成气晕(见图2(a))。对于具有足够内部循环的大液滴,内部成核似乎不太可能,但可能比经典成核理论所建议的更相关。[36]图2(b)所示的反应机理似乎合理,但需要实验验证。
在将本研究中使用的各种内部极限传质模型与Wakao[30]外部极限传质模型进行比较时,值得注意的是,外部传质对总传质影响很小。因此,内部传质是质量交换过程中的速率控制因素(> 95%)。
由于化学反应或聚结引起的液滴质量变化在本工作中未被考虑。由于小液滴停留时间长,导致这些小液滴在吹炼过程中在炉渣中堆积。计算表明,乳状液中含有大量的金属。因此,在模拟乳化液精炼过程时,需要对聚结现象进行建模。随着乳液中金属含量的增加,停留时间明显缩短。液滴的统一导致它们加速被隔离到整体中。
表面活性成分的存在可以促进质量交换。[37]这一现象对整体传质的影响在本工作中没有研究。
上层液滴分布因子根据Kemminger[34]发表的模拟结果计算。在公布的数字中测量了最大的液滴,并计算了相等吹风条件下的值,结果为¼。通过使用Price执行的放射性示踪剂方法从实验中获取的数据进一步验证喷射种群的停留时间,预计在前2/3的吹气时间内,停留时间在¼到1/16之间。使用磷平衡和提出的模型预计在1和1 / 4之间。因此,¼的计算被认为是可行的,可以在全尺寸转化器的液滴尺寸分布模型中实现,而不是2.7[12](小规模验证)。
本文旨在研究转炉过程中金属液滴在炉渣中的停留时间。为此,建立了停留时间的数学模型,并将其与Rout等人的吹数理论和先前提出的液滴尺寸分布模型相结合。本研究的主要结论可以总结如下。
对于工业转炉转化器的研究,Resch[6]和Rout等人[11]的质量抛射模型优于Subagyo等人[7]和Block等人[5]的模型。液滴出口速度是使用这项工作中开发的模型预测的,而Subagyo等人[16]的模型与文献中可用的CFD结果相比可能低得令人难以置信[34]。将液滴粒径分布模型[12]的模型常数修正为¼。胀气现象对停留时间的影响可以忽略不计。
关于脱碳动力学,乳液对总速率的贡献估计小于25%。小液滴(< 2mm)的精炼贡献估计可以忽略不计。在计算条件下,发现金属液滴的反应速率受到内部传质的限制,而与液滴大小无关。
发表评论
暂时没有评论,来抢沙发吧~